
[ad_1]
Manolis Dermitzakis, a professor of genetics at the University of Geneva, disagreed with the EKPA assistant professor’s model for distance in classrooms.
Specifically, on Saturday morning, Mr. Majorkinis had made a post on Facebook where he essentially explained with diagrams why there are no gains from reducing students.
The EKPA Hygiene and Epidemiology teacher explains why school classrooms cannot be evaluated as restaurants.
According to Mr. Majorkinis, the composition of classes is such that we can consider them as bubbles or social bubbles. In fact, due to this composition, in case of transmission of the virus of this class, it is completely traceable and easily limited.
In fact, among other things, the teacher explained with diagrams how much is the distance charge for every 25 students in a class and how much for every 15 students.
The professor’s post-analysis in detail:
After yesterday’s briefing at the Ministry, I go back to class size a bit because the discussion seems to focus there and I explain why I am not convinced it is that important. The 1.5 meter distance is important for droplet transmission and should be observed as closely as possible in general. Where we cannot find a way to reduce the probability of transmission using a mask.
The same logic applies to schools with widespread use of masks in the classroom. It should be noted that classes cannot be considered dining areas. In focus there is a constant alternation of people gathered. Classes always have the same composition, so we can consider them as social “bubbles” or “bubbles”, so the logic in dealing with them is quite different. In principle, any transmission in the classroom is fully traceable and can be limited by a simple restriction, while in focus it creates “orphaned” cases.
A constantly debated issue is: what is the load of distances> 1.5 meters in the classes of 25 students compared to the class of 15 students?
To help explain a bit, I have made a table of classes of 15 students (right). With green arrows I show the 2 distances of the student in the first desk with all the students in the next row (8 distances), for convenience I do not show the rest with students in the same series (6 distances). This student’s distances are 14 and they all exceed 1.5 meters. The total distances in this arrangement are 120.
Graphic
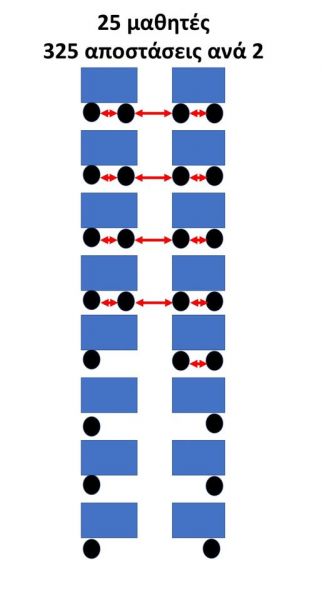
As shown below, a class of 25 students, every 2 distances, is 325 to 13 to exceed the limit of 1.5 meters, that is, only 4% of all possible combinations. These “infractions” are only in the horizontal plane and do not allow transmission to the vertical axis of the order.
Graphic
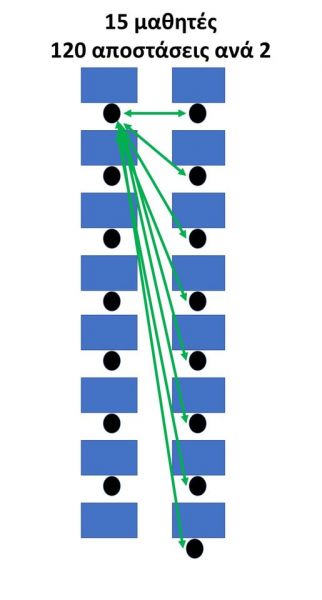
Therefore, from these calculations, converting the class to a size of 15 people eliminates 4% of every 2 distances during the lesson. At the same time, the number of teaching hours to be covered by teachers increases (almost doubles).
So, the scenario shows that for the possibility of transmission exclusively during the educational process in order to lower 4% of the close contacts, you will have to double the exposure time of the teachers.
I understand that intention is always the best of students and teachers, but personally I think the answer is not that simple and I am not entirely sure that there would be (and if there was) a significant gain in reducing the transmission from 25 to 15 in terms of droplet transmission.
The charge
Dermitzaki controversy: “Giga I do not agree with your model”
Commenting on Mr. Majorkinis’ post, his colleague Manolis Dermitzakis expressed his opposition to distance analysis in classrooms, emphasizing that “when you have 25 people in a certain area, you increase the chance that someone will be positive and therefore for transmit to a number of students more and even greater than if the class had 15 people ”.
Comment of Mr. Dermitzakis in detail:
“Gika, I do not agree with your model.” When you have 25 people in a certain area, you increase the possibility that someone will be positive and therefore transmit to a number of other students and even higher than if the class has 15 people “.
“Also, because children are largely asymptomatic, if a positive is found in a class of 25, it will pass silently undetected.”
“Finally, when each class has 25 people, the entrance and exit, as well as the presence at recess will be more crowded than if it were 12 or 15. I think there are many reasons to start classes with half the children until they teachers and managers of their automations, and transition to full classes. “
Reply Mayorkin: Unfortunately, it is not that simple
Mr. Majorkinis’s response was not long in coming, essentially explaining why the area does not play that role, but the distances themselves.
“Unfortunately, it is not that simple. It does not depend on the area but on the two distances and the profit must be quantified in relation to the cost in numbers.” Starting with the rotation makes the educational process enormously difficult.
[ad_2]